Option Methodology

Option Methodology

For European generic options and bond options, we use a payout-adjusted from of the well-known Black-Scholes model. For American options, the software has functions for the binomial and trinomial lattice models, and an approximation algorithm derived by Ho, Stapleton and Subrahmanyam (HSS, see Technical References). The HSS approximation represents an improvement over the Whaley quadratic approximation.

The binomial and trinomial lattice ("tree") models for American options use a control-variate in order to improve accuracy. In this technique, the lattice is used to value two securities simultaneously – the American option under consideration and a European option with the same terms whose value is known analytically using the Black-Scholes equation. The American tree price is adjusted by the amount that the European tree price differs from its known analytic solution.

In general, trinomial models have better convergence properties than binomial models and are more stable numerically. We've included the more common binomial model to facilitate comparison with other software packages. The user can specify the number of steps used in the binomial and trinomial models. There is a tradeoff between computational speed and accuracy – doubling the number of steps causes the computation to slow by a factor of four. Fifty to eighty tree steps should provide very accurate results for almost any practical application. If volatility is very high (say more than 200% per annum), however, the number of tree steps needed to ensure convergence will be much greater (several hundred steps).

Interest rate derivatives such as FRAs, swaps, swaptions, caps and floors are priced to exact days and using a full zero coupon curve methodology. For example, consider a European Payer Swaption (the right to pay fixed). The standard Black-76 futures option model is implemented in the following manner:

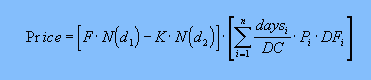
where

F = forward swap rate at the valuation date
K = strike rate of swaption
d₁, d₂ = Black-Scholes risk neutral constants
N() = cumulative standard normal distribution
days_i = exact days over swap coupon period i-1 to i
DC = year basis (e.g. 360 or 365)
P_i = principal outstanding over swap coupon period i-1 to i
DF_i = discount factor at end date of i-th swap coupon (interpolated from relevant curve)
Cap and floor prices are computed in a similar fashion as portfolios of individual caplets and floorlets. Swaption, bond option, and cap/floor prices can also be computed using the Hull-White no-arbitrage yield curve model (see later section of this online help).